FIRE/J - Optimizing Regular Expression Searches with Generative Programming
Vassilios Karakoidas and Diomidis Spinellis
email: {bkarak, dds}@aueb.gr
Athens University of Economics and Business
Department of Management Science and Technology
Patission Ave 74 GR-104 34
Athens, Greece
Abstract
Regular expressions are a powerful tool for analyzing and manipulating text. Their theoretical background lies within automata theory and formal languages. The FIRE/J (Fast Implementation of Regular Expressions for Java) regular expression library is designed to provide maximum execution speed, while remaining portable across different machine architectures. To achieve that, FIRE/J transforms each regular expression into a tailor-made class file, which is compiled directly to Java virtual machine (JVM) bytecodes. The library is compatible with the POSIX standard.
Keywords: Regular Expressions; Just-in Time (JIT); Java; Java Virtual Machine (JVM); Automata; Domain-Specific Languages (DSL); Generative Programming
1 Introduction
Regular expressions are a powerful tool for analyzing and manipulating text. They are very popular among programmers and sophisticated computer users and are integrated in a variety of applications, including text editors (vi, emacs), command line text processing utilities (grep, sed, awk), code generators and tools. They come as standard features in all modern programming languages, such as Java, Perl and Python. Typically, operations using a regular expression have a lifecycle consisting of the following phases:
- Construction of an automaton from the regular expression
- Application of the automaton on the input data
The FIRE/J (Fast Implementation of Regular Expressions in Java) regular expression library is designed to optimize the regular expression execution speed while remaining portable across different machine architectures and compatible with existing Java regular expression implementations. To achieve that, each regular expression is translated into a tailor-made class file, and then it is compiled directly on to Java Virtual Machine (JVM) bytecodes. FIRE/J is compatible with the POSIX standard.
The main contribution of this research is the description of the techniques we have used to eliminate the overhead of run-time automaton interpretation, by compiling it at runtime into a portable, yet efficient, virtual machine representation. Interestingly our approach, coupled with virtual machine just-in-time compilation techniques, can result in better execution performance than that of the traditional C library.
The FIRE/J engine is not related with the regular expression library FIRE, which was developed by Bruce W. Watson in C++ [Wat94].
2 Motivation and Related Work
The theoretical background of regular expressions lies within automaton theory and formal languages. Regular expressions belong to a type 3 grammar of the Chomsky hierarchy. This hierarchy, described by Chomsky in 1956 [Cho56], provides a categorization of grammars that describe formal languages.
In 1943 Warren McCulloch and Walter Pitts described the human neural system using automata [MP43]. The mathematician Stephen Kleene described the proposed models with a mathematical notation named regular sets [Kle56]. Later Brzozowski [Brz64] provided mathematical definitions for the Kleene regular expressions formalism, and introduced ways to convert regular expressions in to state diagrams. In the late 1960s, Ken Thompson proposed a compiler that translated a regular expression into the assembly language of an IBM 7094 processor [Tho68]. Later on, he implemented the regular sets in his text editor named qed, and afterwards on ed, which became part of the UNIX distribution. From then on, regular expressions became widely used in almost all UNIX variants.
Ehrenfeucht and Zeiger [EZ74] provided the academic community with four metrics that measured the complexity of regular expressions. In 1980, Ernst Leiss [Lei80] presented an algorithm for constructing a finite automaton from a given regular expression, and two years later Floyd and Ullman [FU82] proposed an approach for compiling regular expressions into integrated circuits. Sensory Networks [Net04] constructed a content classification accelerator that implements a regular expression engine in hardware.
Regular expressions have also become a standard feature in many programming languages. Programming languages like Java, Ruby and Python contain regular expression engines as part of their API, and, as shown in Section 3, Perl also defines a set of operators and integrates regular expressions into its syntax [WCO00]. In addition, Perl permits a grammar definition with syntactic rules expressed with regular expressions [Zla04]. SQL was extended to use regular expressions patterns in its syntax [Sto03,EM03]. Most modern UNIX variants provide regular expression facilities built into the C library (libc).
In 1992, Wu and Manber [WM92] introduced bit-parallel searching. Navarro and Raffinot introduced in 2005 two new techniques for regular expression searching that produce faster results [NR05]. Their idea is based in bit-parallel matching [WM92,BYG92] and Gluskhov's NFA construction algorithm [Glu61]. This approach is implemented in the NRGrep tool [Nav01]. Navarro [Nav03] also introduced a way of searching text patterns on compressed data.
Regular expressions are mainly used in a variety of software projects as a standard way to perform pattern matching and text validation. Lex [Les75] introduced a method to write lexical analyzers based on regular expressions and automatically generate their code. Nowadays, lex is considered a classic lexical analysis tool [JL87,ASU85]. Clarke and Cormack [CC97] demonstrate a practical way to parse structured text using regular expressions. They also provide an extension rule to regular expressions and a prototype implementation for testing. Spinellis [Spi99] also used regular expressions in his assembly optimizer.
Research to expand regular expressions is also found in literature, usually trying to generate test data that obey specific patterns. Hamilton [Ham88] introduces an algorithm to expand generalized regular expressions, and Wentworth [Wen93] demonstrates a prototype implementation in Haskell.
Although many scientists have worked on improving the performance of regular expression engines, sometimes the bottlenecks lie elsewhere. Hume's Grep Wars [Hum88] is a classic example. In this publication, Hume describes a new I/O library (fio) that was used in the grep utility and improved its performance by a factor of 8.
FIRE/J adopts a standard technique for generating the automaton and introduces a just-in time (JIT) compiler into the regular expression engine that generates tailor made classes for each regular expression. The method we use is referred in the literature as Genesis [Ayc03]. Code generation (specialization) is a classic approach used to cope with certain problem categories [SLC03], such as compilers [Les75,CNL04] and performance enhancement tools [Fri04,Bot98,QEX04].
3 The Mechanics of Regular Expressions
A typical regular expression engine is defined by two main characteristics: (1) engine type and (2) syntax standard. According to their engine type, regular expression implementations can be divided into two main categories [ASU85,Fri02]:
- NFA (Non-deterministic Finite Automaton)
- The engine represents the regular expressions as a non-deterministic finite automaton. NFA-based libraries are generally slower, but allow syntactically richer regular expressions. NFA based engines are categorized into Traditional NFA and POSIX NFA engines. NFA engines have typically slower execution time than DFA [Fri02]. NFA-based engines are known as "regular expression-directed", indicating that the engine dictates the matching process.
- DFA (Deterministic Finite Automaton)
- DFA-based implementations construct a deterministic automaton to represent the regular expression. Deterministic automaton based engines are generally faster and predictable, returning always the longest leftmost match. They are more difficult to implement and lack certain features, such as backtracking. DFA based engines are known as "text-directed".
A finite automaton is a type of graph where nodes represent states and edges represent transitions among them. Each transition has rules that act as prerequisites while traversing the automaton, depending on the input data. Each engine type has different requirements in space and time depending on the regular expression and the input sequence length. If we define as r the regular expression length and n the character input sequence size, the algorithmic complexities of NFA and DFA based engines are shown in Table I [ASU85]. There are also implementations that combine characteristics from these two categories. These are known as hybrid implementations [Fri02].
Table 1: Time & Space complexities for NFA, DFA automaton
|
Automaton Type | Space | Time | Common Implementations |
|---|
|
NFA | O(r) | O(r ×n) | grep, awk, perl, j2sdk |
| DFA | O(2r) | O(n) | tcl, automaton, FIRE/J |
Regular expressions come in three dominant syntax standards. We emphasize here that the syntax does not imply a corresponding engine type. These are:
- Traditional UNIX regular expressions
- POSIX (extended) modern regular expressions
- Perl compatible regular expressions (PCRE)
The traditional UNIX regular expression was the first syntax that was defined and implemented. It has now been replaced by the POSIX standard, although most UNIX applications and utilities, such as sed and grep, provide support for it. Notably, its syntax does not provide the union operator (" - ").
POSIX extended regular expressions [POS03] provide an extension to the aforementioned syntax. Three new operators are introduced: (1) union (" - "), (2) zero or one matching ("?") and (3) one or more matching ("+"). Table II illustrates the most common operators of traditional UNIX and POSIX standards.
POSIX also provides a protable way to define character classes. e.g. [::lower::] is [a-z]. These classes provided a quick and compact way to solve internationalization problems. For example, the Greek language features an alphabet different than the Latin, so in order to write a generic regular expression that matches non-capital alphanumeric characters, an abstract form of character representation is needed to transparently match text according to the system's locale. The Unicode technical committee also proposed a technical standard on Unicode support in regular expression engines [Com04].
Table 2: Typical Regular Expressions Operators
| Operator | Description | Example | TR-Unix | POSIX |
|---|
|
c | character match | a | √ | √ |
| . | Any character match | a.*a | √ | √ |
| [] | Character group definition | [a-z] | √ | √ |
| [^] | Negated group definition | [^a-z] | √ | √ |
| c* | zero or more character match | a* | √ | √ |
| c+ | one or more character match | a+ | × | √ |
| c? | zero or one character match | a? | × | √ |
| ^ | start of line | ^aaab | √ | √ |
| $ | end of line | aaab$ | √ | √ |
| c{x,y} | x minimum to y maximum occurrences of character c | a{1,2} | √ | √ |
| r - c | character r or c match | a - b | × | √ |
Perl compatible regular expressions (PCRE) extend the syntax to provide functions for backreferencing, assertions and conditional subexpressions [WCO00].
Table 3: Regular Expression Examples
| Regular Expression | Example |
|
[1-9][0-9]* | 1, 2, 3, 4, ... |
| ([a-f]) | a, b, c, d, e or f |
| a+ | a, aa, aaa, aaaa, ... |
| (m - n - kn - r)ight | "might", "night","knight" and "right" |
| (([0-9]+)?) - (([0-9A-F]+)?) | 1, 1A, AA, BF, FF, ... |
Table III contains examples of common regular expressions. The first example illustrates a regular expression that matches decimal numbers. Note that the parentheses ("(", ")") have a dual use, it can be used both to define groups and to encapsulate subexpressions. The fifth regular expression provides an example of its usage. An interesting example is the fourth, which depicts how easily we can match with a simple regular expression similar words like might, night, knight or right.
4 Architecture
FIRE/J is developed as a testbed for direct code generation from a regular expression into Java source code and JVM bytecodes. It is compatible with the J2SDK 1.5.x Regular Expression Application Programming Interface (API). Currently, the FIRE/J library implements the POSIX standard.
Regular expressions can be considered as a domain-specific language (DSL) that deals with the text-parsing and manipulation. All regular expression libraries in Java are designed using the piggyback pattern, as Spinellis categorized in [Spi01], where a DSL is being designed on top of an existing host language. FIRE/J is designed using the source-to-source transformation creational pattern, where a DSL is compiled into the host language code, which in our case are JVM instructions.
Figure 1 illustrates the architecture of our implementation. FIRE/J accepts as input a regular expression, and generates a compiled Java class as output. Internally, it consists of five distinct components; (1) a Preprocessor, (2) a Compiler, (3) a Code Generation Back-ends, (4) a Regular Expression Caching Engine and (5) a Buffer Subsystem.
Figure 1: Architecture of FIRE/J Engine
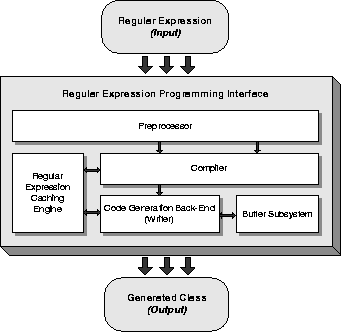 The preprocessor translates regular expressions macros, such as character classes, into a simpler form. For example, the character class "\p{Alpha}" is automatically replaced by its equivalent [a-zA-Z]. This component is also used for internationalization. If the locale is correctly set, then the aforementioned character class will be replaced with the appropriate locale specific range e.g. in Greek, \p{Alpha} should be [a-wA-W]. The preprocessor can also be extended to work at the regular expression syntax level e.g. the expression ab+a can be translated into its equivalent abb*a. The compiler constructs a DFA from the simplified regular expression.
Code generation back-ends translate the generated automaton into specific code. In the FIRE/J distribution, we provide two types of back-ends: an experimental that writes Java code and the production one that directly generate JVM bytecodes.
Code generation and runtime class assembling proved to be an expensive procedure. To cope with the problem we implemented a caching layer. The regular expression caching engine provides a transparent mechanism to store the processed regular expressions and retrieve them when necessary. The way it works is similar to the compile once ("o") switch in Perl's operator "m//" [WCO00] and the CompileToAssembly method in the standard .NET regular expression library. The engine provides caching for both the compiler and the code generation back-end modules. The regular expression caching engine is a singleton object [GHJV94] and has only one instance per virtual machine. Consequently cached objects, such as instances of compiled regular expression can be accessed by any application in the virtual machine using our regular expression library, and benefit by the precompiled regular expressions. This feature has significant performance improvement in server-side applications, like web servers and servlet/JSP engines, such as Tomcat, where server and applications share the same JVM.
The buffer subsystem provides a standard means of accessing the input data that will be parsed. In order to improve performance, it is tightly integrated with the generated Java class. This layer is optional; therefore a module developer could override it, and implement his/her own buffering strategy.
FIRE/J generates code in order to provide performance optimization in the execution of each regular expression and it could be compared with other code generators, such as lex [Les75], jlex [BA03], flex or their Java-based clone jflex. FIRE/J shares some common characteristics with such tools:
The preprocessor translates regular expressions macros, such as character classes, into a simpler form. For example, the character class "\p{Alpha}" is automatically replaced by its equivalent [a-zA-Z]. This component is also used for internationalization. If the locale is correctly set, then the aforementioned character class will be replaced with the appropriate locale specific range e.g. in Greek, \p{Alpha} should be [a-wA-W]. The preprocessor can also be extended to work at the regular expression syntax level e.g. the expression ab+a can be translated into its equivalent abb*a. The compiler constructs a DFA from the simplified regular expression.
Code generation back-ends translate the generated automaton into specific code. In the FIRE/J distribution, we provide two types of back-ends: an experimental that writes Java code and the production one that directly generate JVM bytecodes.
Code generation and runtime class assembling proved to be an expensive procedure. To cope with the problem we implemented a caching layer. The regular expression caching engine provides a transparent mechanism to store the processed regular expressions and retrieve them when necessary. The way it works is similar to the compile once ("o") switch in Perl's operator "m//" [WCO00] and the CompileToAssembly method in the standard .NET regular expression library. The engine provides caching for both the compiler and the code generation back-end modules. The regular expression caching engine is a singleton object [GHJV94] and has only one instance per virtual machine. Consequently cached objects, such as instances of compiled regular expression can be accessed by any application in the virtual machine using our regular expression library, and benefit by the precompiled regular expressions. This feature has significant performance improvement in server-side applications, like web servers and servlet/JSP engines, such as Tomcat, where server and applications share the same JVM.
The buffer subsystem provides a standard means of accessing the input data that will be parsed. In order to improve performance, it is tightly integrated with the generated Java class. This layer is optional; therefore a module developer could override it, and implement his/her own buffering strategy.
FIRE/J generates code in order to provide performance optimization in the execution of each regular expression and it could be compared with other code generators, such as lex [Les75], jlex [BA03], flex or their Java-based clone jflex. FIRE/J shares some common characteristics with such tools:
- Code Generation
- All the above tools generate code according to a regular expression based syntax.
- Automaton Based
- FIRE/J and lexical analyzers generate code that represents a finite automaton.
It has also several differences:
- Scope
- FIRE/J as a regular expression engine has a very narrow scope. Lex variants on the other hand are used for lexical analysis. Lex could have a FIRE/J engine embedded as a building block.
- Target Code
- Lex generates high-level code (Java and C) and depends on the compiler to generate the executable code, while FIRE/J generates JVM bytecodes.
- Run-time vs. Compile-time
- FIRE/J is generating the executable code at run-time, while lex generates source code that is statically linked in a bigger program, or compiled and executed separately.
5 Code Generation
State machines are typically implemented either as a large switch statement, where each case represents a different case, or through code blocks linked together via goto statements. The switch-based method is easier to implement with integer-based lookup tables, but incurs the overhead of an additional level of indirection-the mapping from the integer identifier of the state to the corresponding machine address containing the code. To avoid this overhead and get around the fact that Java lacks a goto statement, FIRE/J generates code as portable machine instructions. As an aid to debugging and to measure the improvement of the JVM code generation technique, we also implemented a back-end that writes switch-based code in Java.
5.1 Generating Java Source
The Java generator compiles the given DFA directly into Java source code. Then, the Java compiler is invoked. Algorithm 1 shows the basic structure of the generated code, which follows the same principles described by Thompson [Tho68] and adopted by code generators such as lex [Les75] and jlex [BA03].
Algorithm 1: Generated code structure for a goto-less language
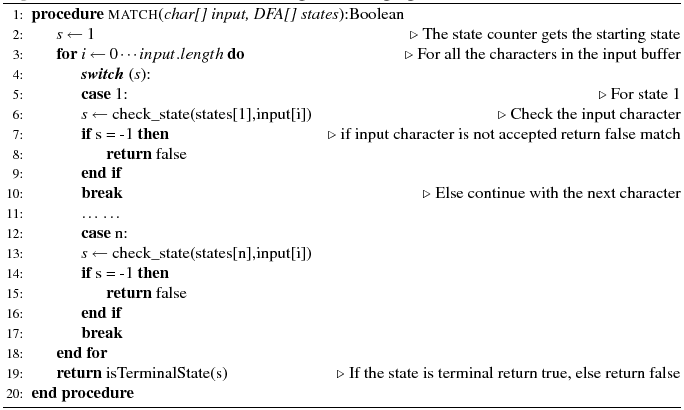 The algorithm receives as input a character sequence and the DFA states array, and returns a Boolean value indicating if a full match has been achieved. The generated code is a big loop with a switch - case statement. Starting from the initial state, all the characters in the input buffer are being checked against the transition rules of the DFA states. If a character does not satisfy the selected state, then the match fails and the procedure exits. When the input buffer runs out of character data, the last visited state is checked. If the state is terminal then the procedure returns true; otherwise it returns false. The structure of this algorithm is similar to the code generated by the lexical analyzer lex. In our implementation we have inlined all the methods, such as check_state and isTerminalState, in order to avoid the method call overhead [McC06,p601].
The algorithm receives as input a character sequence and the DFA states array, and returns a Boolean value indicating if a full match has been achieved. The generated code is a big loop with a switch - case statement. Starting from the initial state, all the characters in the input buffer are being checked against the transition rules of the DFA states. If a character does not satisfy the selected state, then the match fails and the procedure exits. When the input buffer runs out of character data, the last visited state is checked. If the state is terminal then the procedure returns true; otherwise it returns false. The structure of this algorithm is similar to the code generated by the lexical analyzer lex. In our implementation we have inlined all the methods, such as check_state and isTerminalState, in order to avoid the method call overhead [McC06,p601].
5.2 Generating Bytecodes
The basic structure of the bytecode writer is listed as Algorithm 2. The code imposes the same logic as the one described in the previous algorithm. Their main difference lies in the state selection procedure. When using low-level JVM instructions, the goto instruction can be used. By using it, each state jumps directly to the appropriate memory address, instead of executing the switch statement used in Algorithm 1.
Algorithm 2: Generated code structure with goto
 If we define as n the number of states of the automaton, and m the size of the character sequence for the Algorithm 1, a total of n ×m of steps are needed to perform a full match, if the switch is naively compiled as a linear sequence of test and branch instructions. Consequently, the complexity of Algorithm 1 is O(n×m). For Algorithm 2, the required steps would be O(m), because each state jumps directly to the next or fails. We will see in section 6 that this technique provides significant performance gains.
If we define as n the number of states of the automaton, and m the size of the character sequence for the Algorithm 1, a total of n ×m of steps are needed to perform a full match, if the switch is naively compiled as a linear sequence of test and branch instructions. Consequently, the complexity of Algorithm 1 is O(n×m). For Algorithm 2, the required steps would be O(m), because each state jumps directly to the next or fails. We will see in section 6 that this technique provides significant performance gains.
6 Benchmarking
The benchmark process consists of two separate experiments. For overall performance evaluation, we benchmark expressions that are used in everyday programs. In addition, we also evaluate two specialized regular expressions against small buffers: an IP address matcher (medium size/complexity) and an Apache log entry (large size/complexity).
Each test is executed separately. Thus, we guarantee that each test will run isolated and its performance will not be affected by any previous executions. In addition, we perform a warm-up period for the virtual machine in order to eliminate overhead, such as class bytecode verification and also give the JIT the opportunity to compile frequently used methods in to native code. Each Java benchmark is also executed in a separate virtual machine process.
In order to obtain accurate time values we used the method System.currentTimeMillis(), which according to literature is the most efficient and correct method to use in similar cases [Shi03]. The caching engine of FIRE/J was deactivated during the experiment. The benchmark was executed on a Pentium 4 CPU at 2.8 GHZ with 512 Megabytes of memory. The underlying operating system was a Linux distribution with the 2.6.16 kernel version.
6.1 Evaluation Criteria
To theoretically support our results we adopted two complexity metrics that were introduced by Andrej Ehrenfeucht and Paul Zeiger in 1974 [EZ74]. Using these we can categorize and compare the regular expressions we use in throughout our benchmarking process.
- Size (S)
- Number of alphabetical symbols in the expression
- Length (L)
- Length of longest non-repeating path through the expression
The Size complexity metric represents the number of states and transitions of the generated automaton, while Length indicates the number of minimum steps an engine has to perform in order to achieve a match.
- Compile Time (tcomp)
- overhead indicates the time required by an engine to parse a regular expression and generate the automaton. For the FIRE/J engine this includes the time of the JIT compilation.
- Execution Time (tmatch)
- indicates regular expression engine match efficiency. It represents the amortized execution time of a single compiled regular expression against specified text.
- Break-even point
- indicates the number of executions that must be performed in order to cover the compile time difference between two regular expression engines. To calculate it, we used the following function:
where tmatch represents the execution time of the regular expression engine, tcomp the compile time and r the number of invocations. The break-even point is calculated as the number of invocations r that satisfies the following equation:
The results of our experiments are illustrated as graphs of the execution time against the length and size for each regular expression, thus providing the means to relate execution time with these, more abstract characteristics. As a result, we investigate how the size of the generated automaton, and the number of matching steps involved affects overall performance.
6.2 Benchmark Participants
Our benchmarks include the Sun regular expressions engine [SUN03] (J2SDK) as the most fully featured engine indicated
by the bibliography [Fri02] and practitioners, and the Automaton engine (Automaton) as the only DFA engine [Moe03]. Other Java implemented engines such as GNU regexp [GNU01b], Jakarta regexp [Loc04] and Jakarta ORO [Sav04] were tested and finally not included in the benchmark, because their performance was not exceptional.
We also found interesting to include non-Java platforms. We chose the MONO implementation [Com05] as another virtual machine based platform, Perl [WCO00,Haz06], the GNU regular expression library in C [GNU01a] and Henry Spencer's library [Spe07]. All the above regular expression libraries are NFA-based implementations and follow the POSIX standard, with the exception of Perl, which supports PCRE. The benchmarking environment included the 1.5.0 (build 9) version of the Java Runtime environment, 5.8.8 version of Perl, the 1.1.13.8 version of MONO implementation, the 1.8-8 version of the automaton library and the alpha 3.8 of the Henry Spencer's library.
We targeted our benchmark mainly on regular expression engines and not tools like GNU grep, AGrep
and NRGrep. Although those tools provide fast implementations and interesting variations of regular expression execution engines, it is too difficult to isolate the overhead of their execution time. These libraries have their engines integrated with the whole tool, making it almost impossible to get precise results for the engine part without the accompanying overhead.
6.3 Real-World Regular Expressions
In our experiments we used 849 of real-world regular expressions that were obtained from the regexlib1 web site. The average occurrence of each regular expression operator for our data set is listed on Table IV. Descriptive statistical measures for our data set are presented in Table VI.
Table 4: Average Operator Occurrence
| Operator | Occurrence |
|---|
|
. | 0 | .15 |
| + | 0 | .58 |
| * | 0 | .7 |
| ? | 1 | .39 |
| - | 3 | .85 |
| () | 5 | .08 |
| [] | 7 | .32 |
None of the engines had 100% compatibility with our data set. The success rates of our participants are illustrated on Table V. Noticeably; FIRE/J has the lowest success rate than all the engines. FIRE/J uses the Automaton DFA compiler, which bounds its success rate to 685 (as shown in Table V). As we will see later on, this decision was based only on our need to isolate the performance gain of the code generation optimization.
Table 5: Participants Success Rate (Total 849)
| | Succeeded | Ratio |
|---|
|
J2SDK (Java) | 805 | 95 |
| Automaton (Java) | 685 | 81 |
| FIRE/J - Java (Java) | 665 | 78 |
| FIRE/J - bytecode (Java) | 665 | 78 |
| GNU (C) | 760 | 90 |
| Spencer (C) | 721 | 85 |
| Mono (C#) | 788 | 92 |
| Perl | 792 | 93 |
Table 6: Statistical Measures
| | 1st Quartile | Avg. | Median | 3rd Quartile | Max |
|---|
|
Size | 68 | 301 | 153 | 372 | 3394 |
| Length | 10 | 20 | 17 | 26 | 136 |
We narrowed down our results only to the common success cases and then performed linear regression to be able to compare them directly. The common successful cases were 629. We provide four performance charts (Figure 2, 3, 4 and 5) to compare the FIRE/J bytecode implementation with the other participants. The charts show the execution time (Y axis) related to the size and length.
As one can see from the graphs that FIRE/J is the fastest engine, having in general faster execution times than all its competitors. The Automaton engine is the second fastest participant. This was expected, because it is the only engine except FIRE/J that is based on a DFA. Surprisingly, the native libraries we tested were significantly slower. Those results can be explained having in mind the following two factors: (a) the engines are based on NFAs and (b) they were implemented many years before, and modern programming abstractions and techniques were not used in their implementations. The Spencer engine proved
to have poor performance and was excluded from the graphs. Table VII lists some common statistical measures calculated from our results.
Figure 2: Matching Performance for Java engines - Execution time / Size (S)
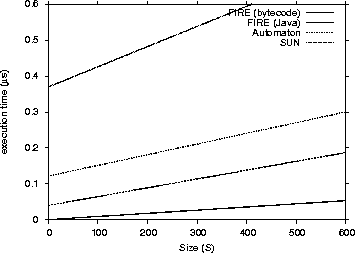 Figure 3: Matching Performance for non-Java engines - Execution Time / Size (S)
Figure 3: Matching Performance for non-Java engines - Execution Time / Size (S)
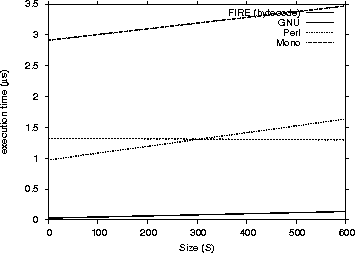 Figure 4: Matching Performance for Java engines - Execution Time / Length (L)
Figure 4: Matching Performance for Java engines - Execution Time / Length (L)
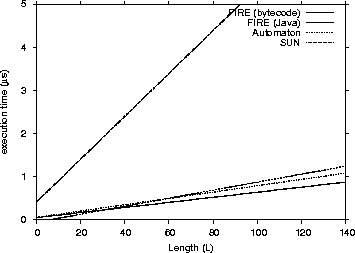 Figure 5: Matching Performance for non-Java engines - Execution Time / Length (L)
Figure 5: Matching Performance for non-Java engines - Execution Time / Length (L)
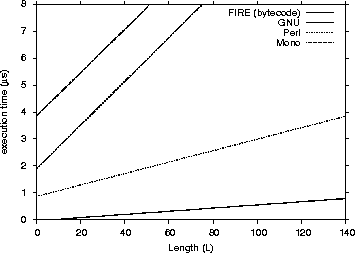 Table 7: Matching Performance Statistical Measures (ms)
Table 7: Matching Performance Statistical Measures (ms)
| Engine | 1st Quartile | avg | median | 3rd Quartile | max |
|---|
|
J2SDK (Java) | 132 | 357 | .92 | 227 | 371 | 69310 |
| Automaton (Java) | 115 | 200 | .78 | 177 | 253 | 1191 |
| FIRE/J - Java (Java) | 40 | 124 | .28 | 67 | 134 | 3039 |
| FIRE/J - bytecode (Java) | 33 | 75 | .45 | 50 | 72 | 4351 |
| GNU (C) | 120 | 1135 | .69 | 980 | 1630 | 18440 |
| Spencer (C) | 230 | 2497 | .87 | 680 | 2680 | 108700 |
| Mono (C#) | 434 | 928 | .59 | 667 | 1072 | 8004 |
| Perl | 90 | 128 | .08 | 107 | 144 | 672 |
6.4 Hand Crafted Regular Expressions
We also performed two tailored tests with hand-crafted expressions, a typical matching example and a more complex regular expression. As our first case we used a regular expression that matches an IP address (IPV4) [Fri02].
(([01]?[0-9][0-9]?|2[0-4][0-9]|25[0-5])\\.){3}([01]?[0-9][0-9]?|2[0-4][0-9]|25[0-5])
The second regular expression involves a verifier for an Apache web server log entry:
([0-9]{1,3}\\.){3}[0-9]{1,3}[ \\-]+.[0-9]{1,2}/[a-zA-Z]{3}/[0-9]{4}:[0-9]{2}:[0-9]{2}
:[0-9]{2}[ ]\\+[0-9]{4}.[ ].(GET|POST)[ ][a-zA-Z/~0-9.%]+[ ]HTTP/[1-9]\\.[1-9]{1,2}.
[ ][0-9]+[ ][0-9]+[ ].-.[ ].[a-zA-Z0-9./]+[ ]\\(.+\\)[ ][a-zA-Z/0-9]+[ ][a-zA-Z/.0-9]+.
The data we used included were a 15-character IP address (255.255.255.255) and an Apache log entry of 193 characters length. Table VIII shows the results of the benchmark process. As we can see the FIRE/J engine is faster than all its competitors.
It is also interesting to note, that the FIRE/J-Java generator loses slightly from the automaton engine in the more complex regular expression. Our experiments showed that the FIRE/J-Java generator loses matching speed when the DFA has many states. In this case the generated class file is very big in terms of size, which causes cache misses that compromise the overall performance of the engine. The FIRE/J-bytecode generator will have eventually the same performance problem for more complex regular expressions.
Table 8: Matching Performance (ms)
| | IPv4 | Apache Log |
|---|
|
J2SDK (Java) | 3 | .5 | 33 | .8 |
| Automaton (Java) | 0 | .3 | 4 | .6 |
| FIRE/J - Java (Java) | 0 | .2 | 4 | .9 |
| FIRE/J - bytecode (Java) | 0 | .1 | 1 | .2 |
| GNU (C) | 9 | .2 | 67 | .4 |
| Spencer (C) | 118 | .4 | 7094 | .8 |
| Mono (C#) | 14 | .5 | 39 | .0 |
| Perl | 3 | .8 | 6 | .0 |
6.5 Calculating Compilation Overhead
The compilation benchmark process was simple; we calculated the average compilation time for the Apache log expression (see Section 6.4). The caching modules of FIRE/J were disabled during the experiment. The break-even point is defined as the number of matches that each engine has to execute in order to cover the compile time overhead.
As shown in Table IX, Perl has the fastest compile time. J2SDK, GNU and MONO will never break even against Perl, since they had slower matching performance (see Section 6.4). Automaton will cover the compilation overhead after 32,280 matching invocations and FIRE/J-bytecode after 24,313.
Our implementation uses the Automaton engine for the translation of each regular expression to the DFA. To isolate the overhead of our optimization technique we compiled the regular expression with Automaton and FIRE/J, which includes the code generation, and subtracted the compilation times. According to our benchmarks, the overhead time of the DFA to native code was approximately 217 ms for Java source generation and 72 ms for bytecode generation; about 83% and 62% of the total compilation time.
Table 9: Compilation Performance (ms)
| Engine | Compile Time | Break-even point |
|---|
|
J2SDK (Java) | 62 | .0 | n/a |
| Automaton (Java) | 43,992 | .0 | 32,280 |
| FIRE/J - Java (Java) | 260,904 | .0 | 247,255 |
| FIRE/J - bytecode (Java) | 115,690 | .0 | 24,313 |
| GNU (C) | 160 | .4 | n/a |
| Spencer (C) | 62 | .0 | n/a |
| Mono (C#) | 5 | .3 | n/a |
| Perl | 0 | .9 | 0 |
7 Conclusions - Future Work
The benchmarking experiment demonstrated that the FIRE/J engine is the fastest among its participants. Its main rival is the Automaton engine, as the only DFA engine included in the benchmark. FIRE/J uses the DFA engine of the automaton, so the difference in performance comes only from our optimization, which is the bytecode generation and the use of the goto statement.
Compilation time results indicate that FIRE/J is the slowest engine. This was also expected, since it integrates the regular expression parser of the Automaton. Automaton and FIRE/J generate a DFA automaton. In addition, FIRE/J generates and compiles classes on the fly, a procedure that causes significant overhead. Eliminating the compilation overhead was outside the scope of our work, which focused on how applications like a regular expression engine can benefit from a code generation technique and low level programming traits.
Our main contribution is the description of techniques we used to eliminate the overhead of run-time automaton interpretation, resulted in a performance higher than the C implementation, while remaining machine independent and portable. Portability is our main issue here, because our optimization also provides benefit against native code, even if its based on the assembly language of a higher level virtual execution environment.
FIRE/J is still an experimental engine and has room for improvements. In its current state, it is advisable to use FIRE/J in server side applications or applications that perform intensive regular expression matching, such as log analyzers. In the future we intend to optimize the compile procedure, building a custom based DFA-generator.
Acknowledgments
The authors would like to thank Panagiotis Louridas, Dimitrios Liappis, Aggeliki Tsohou and Marianthi Theocharidou for their insightful comments and corrections during the compilation of this paper. Georgios Gousios and Vassilios Vlachos also supported the writing process with their comments and ideas. Finally, we would also like to thank Stefanos Androutsellis-Theotokis for his artistic touch in many figures of our paper. We would like also to thank the anonymous referees for their valuable comments during the writing process.
References
- [ASU85]
-
Alfred V. Aho, Ravi Sethi, and Jeffrey D. Ullman.
Compilers: Principles, Techniques and Tools.
Addison-Wesley, Reading, MA, 1985.
- [Ayc03]
-
John Aycock.
A Brief History of Just-In-Time.
ACM Computing Surveys, 35(2):97-113, June 2003.
- [BA03]
-
Elliot Berk and C. Scott Ananian.
Jlex: A lexical analyzer generator for java, 2003.
Available online at
http://www.cs.princeton.edu/~appel/modern/java/JLex/.
- [Bot98]
-
P. Bothner.
Kawa - Compiling Dynamic Languages to the Java VM.
In Proceedings of the USENIX Technical Conference,
FREENIX Track. The USENIX Association, June 1998.
- [Brz64]
-
J. A. Brzozowski.
Derivatives of Regular Expressions.
Journal of the ACM, 11(4):481-494, 1964.
- [BYG92]
-
Ricardo Baeza-Yates and Gaston H. Gonnet.
A new approach to text searching.
Communications of the ACM, 35(10):74-82, 1992.
- [CC97]
-
Charles L. A. Clarke and Gordon V. Cormack.
On the Use of Regular Expressions for Searching Text.
ACM Transactions on Programming Languages and
Systems, 19(3):413-426, 1997.
- [Cho56]
-
Noam Chomsky.
Three Models For the Description of Language.
IEEE Transactions On Information Theory,
2(3):113-124, 1956.
- [CNL04]
-
R. G. G. Cattell, Joseph M. Newcomer, and Bruce W. Leverett.
Code Generation in a Machine-Independent Compiler.
ACM SIGPLAN Notices, 39(4):1-13, 2004.
- [Com04]
-
Unicode Technical Commitee.
Unicode Technical Standard: Unicode Regular Expressions,
2004.
Available online at http://www.unicode.org/reports/tr18/.
- [Com05]
-
MONO Community.
The MONO Project, November 2005.
Available online at http://www.mono-project.com/.
- [EM03]
-
Andrew Eisenberg and Jim Melton.
SQL:1999, Formerly Known As SQL3, 2003.
Available online at http://dbs.uni-leipzig.de/en/lokal/standards.pdf.
- [EZ74]
-
Andrzej Ehrenfeucht and Paul Zeiger.
Complexity Measures For Regular Expressions.
In STOC '74: Proceedings of the Sixth Annual ACM
Symposium On Theory of Computing, pages 75-79, New York, NY,
USA, 1974. ACM Press.
- [Fri02]
-
Jeffrey E. F. Friedl.
Mastering Regular Expressions 2nd Edition.
O'Reilly and Associates, Inc., Sebastopol, CA, 2002.
- [Fri04]
-
Matteo Frigo.
A Fast Fourier Transform Compiler.
SIGPLAN Not., 39(4):642-655, 2004.
- [FU82]
-
Robert W. Floyd and Jeffrey D. Ullman.
The compilation of Regular Expressions Into Integrated
Circuits.
Journal of the ACM, 29(3):603-622, 1982.
- [GHJV94]
-
Erich Gamma, Richard Helm, Ralph Johnson, and John Vlissides.
Design Patterns: Elements of Reusable Object-Oriented
Software.
Addison-Wesley, Indianapolis, IN 46920, 1994.
- [Glu61]
-
V-M. Glushkov.
The Abstract Theory of Automata,.
Dussian Mathematical Surveys, 16:1-53, 1961.
- [GNU01a]
-
Regex - GNU Regex Library, 2001.
Available online at http://directory.fsf.org/regex.html.
- [GNU01b]
-
Regular Expressions For Java, October 2001.
Available online at http://www.gnu.org/.
- [Ham88]
-
Eric Hamilton.
Literate Programming-Expanding Generalized Regular
Expressions.
Commucations of the ACM, 31(12):1376-1385, December 1988.
- [Haz06]
-
Philip Hazel.
Perl Compatible Regular Expressions, 2006.
Available online at http://www.pcre.org/.
- [Hum88]
-
Andrew Hume.
Grep Wars: The Strategic Search Initiative.
In Peter Collinson, editor, Proceedings of the EUUG Spring
88 Conference, pages 237-245, Buntingford, UK, 1988. European UNIX
User Group.
- [JL87]
-
Stephen C. Johnson and Michael E. Lesk.
Language Development Tools.
Bell System Technical Journal, 56(6):2155-2176,
July-August 1987.
- [Kle56]
-
Stephen C. Kleene.
Represenations of Events in Nerve Nets and Finite
Automata, volume 34 of Annals of Mathematics Studies, pages
3-42.
Princeton University Press, Princeton, NJ, 1956.
- [Lei80]
-
Ernst Leiss.
Constructing a Finite Automaton For a Given Regular
Expression.
ACM SIGACT News, 12(3):81-87, 1980.
- [Les75]
-
Michael E. Lesk.
Lex-A Lexical Analyzer Generator.
Computer Science Technical Report 39, Bell Laboratories,
Murray Hill, NJ, October 1975.
- [Loc04]
-
Jonathan Locke.
Jakarta Regexp, July 2004.
Available online at http://jakarta.apache.org/regexp/index.html.
- [McC06]
-
Steve McConnell.
Code Complete.
Microsoft Press, 2nd edition, 2006.
- [Moe03]
-
Anders Moeller.
Automaton Library Generated Javadocs, May 2003.
Available online at http://www.brics.dk/automaton/doc/index.html.
- [MP43]
-
Warren S. McCulloch and Walter Pitts.
A Logical Calculus of the Ideas Immanent in Nervous
Activity.
5:18-27, 1943.
- [Nav01]
-
G. Navarro.
NR-Grep: a Fast and Flexible Pattern-Matching Tool.
Softw. Pract. Exper., 31(13):1265-1312, 2001.
- [Nav03]
-
G. Navarro.
Regular Expression Searching On Compressed Text.
J. of Discrete Algorithms, 1:423-443, 2003.
- [Net04]
-
Sensory Networks.
Nodalcore C Series - Content Classification Accelerator,
September 2004.
Available online at http://sensorynetworks.com/.
- [NR05]
-
G. Navarro and M. Raffinot.
New Techniques For Regular Expression Searching.
Algorithmica, 41(2):89-116, 2005.
- [POS03]
-
The Single Unix Specification, Version 3, 2003.
http://www.unix.org/version3/.
- [QEX04]
-
GNU's Qexo (Kawa-Query), 2004.
Available online at http://www.qexo.org/.
- [Sav04]
-
Daniel F. Savarese.
Jakarta ORO, July 2004.
Available online at http://jakarta.apache.org/oro/index.html.
- [Shi03]
-
Jack Shirazi.
Java Performance Tuning.
O'Reilly and Associates, Inc., Sebastopol, CA, 2003.
- [SLC03]
-
Ulrik P. Shultz, Julia L. Lawall, and Charles Consel.
Automatic Program Specialization For Java.
ACM Transactions on Programming Languages and
Systems, 25(4):452-499, July 2003.
- [Spe07]
-
Henry Spencer.
regex - Henry Spencer's regular expression libraries, January
2007.
Available online at http://arglist.com/regex/.
- [Spi99]
-
Diomidis Spinellis.
Declarative Peephole Optimization using String Pattern
Matching.
ACM SIGPLAN, 34(2):47-51, February 1999.
- [Spi01]
-
Diomidis Spinellis.
Notable Design Patterns for Domain Specific Languages.
Journal of Systems and Software, 56(1):91-99, February 2001.
- [Sto03]
-
Knut Stolze.
Bringing the Power of Regular Expression Matching to Ssql,
January 2003.
Available online at
http://www-106.ibm.com/developerworks/db2/library/techarticle/0301stolze/0301stolze.html.
- [SUN03]
-
J2SDK Regular Expressions Engine 1.4.X, 2003.
Available online at http://java.sun.com/j2se/1.4/.
- [Tho68]
-
Ken Thompson.
Regular Expression Search Algorithm.
Communications of the ACM, 11(6):419-422, June 1968.
- [Wat94]
-
B. Watson.
Design and Implementation of the FIRE Engine: A C++
Toolkit For Finite Automata and Regular Expressions, The, 1994.
- [WCO00]
-
Larry Wall, Tom Christiansen, and Jon Orwant.
Programming Perl.
O'Reilly, Sebastopol, CA, 2000.
- [Wen93]
-
E. P. Wentworth.
Generalized Regular Expressions: a Programming Exercise in
Haskell.
SIGPLAN Not., 28(5):49-54, 1993.
- [WM92]
-
Sun Wu and Udi Manber.
Fast text searching: allowing errors.
Communications of the ACM, 35(10):83-91, 1992.
- [Zla04]
-
Teodor Zlatanov.
Perl 6 Grammars and Regular Expressions, 2004.
Available online at
http://www-106.ibm.com/developerworks/linux/library/l-cpregex.html?ca=dgr-lnxw01Perl6Gram.
Footnotes:
1
http://www.regexlib.com


 The algorithm receives as input a character sequence and the DFA states array, and returns a Boolean value indicating if a full match has been achieved. The generated code is a big loop with a switch - case statement. Starting from the initial state, all the characters in the input buffer are being checked against the transition rules of the DFA states. If a character does not satisfy the selected state, then the match fails and the procedure exits. When the input buffer runs out of character data, the last visited state is checked. If the state is terminal then the procedure returns true; otherwise it returns false. The structure of this algorithm is similar to the code generated by the lexical analyzer lex. In our implementation we have inlined all the methods, such as check_state and isTerminalState, in order to avoid the method call overhead [McC06,p601].
The algorithm receives as input a character sequence and the DFA states array, and returns a Boolean value indicating if a full match has been achieved. The generated code is a big loop with a switch - case statement. Starting from the initial state, all the characters in the input buffer are being checked against the transition rules of the DFA states. If a character does not satisfy the selected state, then the match fails and the procedure exits. When the input buffer runs out of character data, the last visited state is checked. If the state is terminal then the procedure returns true; otherwise it returns false. The structure of this algorithm is similar to the code generated by the lexical analyzer lex. In our implementation we have inlined all the methods, such as check_state and isTerminalState, in order to avoid the method call overhead [McC06,p601].
 If we define as n the number of states of the automaton, and m the size of the character sequence for the Algorithm 1, a total of n ×m of steps are needed to perform a full match, if the switch is naively compiled as a linear sequence of test and branch instructions. Consequently, the complexity of Algorithm 1 is O(n×m). For Algorithm 2, the required steps would be O(m), because each state jumps directly to the next or fails. We will see in section 6 that this technique provides significant performance gains.
If we define as n the number of states of the automaton, and m the size of the character sequence for the Algorithm 1, a total of n ×m of steps are needed to perform a full match, if the switch is naively compiled as a linear sequence of test and branch instructions. Consequently, the complexity of Algorithm 1 is O(n×m). For Algorithm 2, the required steps would be O(m), because each state jumps directly to the next or fails. We will see in section 6 that this technique provides significant performance gains.



